一．概述

       图论（Graph Theory）是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些实体之间的某种特定关系，用点代表实体，用连接两点的线表示两个实体间具有的某种关系。
       相比矩阵、张量、序列等结构，图结构可以有效建模和解决社会关系、交通网络、文法结构和论文引用等需要考虑实体间关系的各种实际问题。（关键词：实体间关系）

二．图的基本表示（Graph Representations）
图（Graph）
       图可以被表示为 G={V, E}，其中 V={v1, ... , vN}，E= {e1, ... , eM}。（也就是说，V是节点的集合，即所谓的点集，E是连接两点的线即两点间关系的集合，即所谓的边集）

      在顶点集合所包含的若干个顶点之间，可能存在着某种两两关系——如果某两个点之间的确存在这样的关系的话，我们就在这两个点之间连边，这样就得到了边集的一个成员，也就是一条边。对应到社交网络中，顶点就是网络中的用户，边就是用户之间的好友关系。

       如果用边来表示好友关系的话，对于微信这种双向关注的社交网络没有问题，但是对于微博这种单向关注的要如何表示呢？

      于是引出了两个新的概念：有向边和无向边。

       简而言之，一条有向边必然是从一个点指向另一个点，而相反方向的边在有向图中则不一定存在；而有的时候我们并不在意构成一条边的两个顶点具体谁先谁后，这样得到的一条边就是无向边。就像在微信中，A是B的好友，那B也一定是A的好友，而在微博中，A关注B并不意味着B也一定关注A。

       对于图而言，如果图中所有边都是无向边，则称为无向图，反之称为有向图。（反之有误，因为所有边都是无向边的否命题是，存在有向边。）

        一般而言，我们在数据结构中所讨论的图都是有向图，因为有向图相比无向图更具有代表性。实际上，无向图可以由有向图来表示。如果AB两个点之间存在无向边的话，那用有向图也可以表示为AB两点之间同时存在A到B与B到A两条有向边。

        我们来形式化地定义一下图：图是由顶点集合（简称点集）和顶点间的边（简称边集）组成的数据结构，通常用G(V,E)来表示。其中点集用V(G) 来表示，边集用 E(G) 来表示。在无向图中，边连接的两个顶点是无序的，这些边被称为无向边。例如下面这个无向图G，其点集V(G)={1,2,3,5,6}，边集为E(G)={(1,2),(2,3),(1,5),(2,6),(5,6)}。（无向边的表达方式，元素的先后对边的表示并不影响，（2，6）与（6，2）相同）

        而在有向图中，边连接的两个顶点之间是有序的。箭头的方向就表示有向边的方向。

例如下面这张有向图G'：

        其点集V(G′)={1,2,3,5,6}，边集为E(G′)={(1,2),(2,3),(2,6),(6,5),(1,5)}。对于每条边 (u,v) ，我们称其为从u到v的一条有向边，u是这条有向边的起点，v 是这条有向边的终点。注意在有向图中，(u,v) 和 (v,u) 是不同的两条有向边。（注意有向边的表达方式，前一个元素一定是起点，后一个元素是终点）（有向边与无向边类似于数学中的线段与向量）

三．图的分类（Types）

       有很少边或弧(如e< n log n , e 指边数,n指顶点数）的图称为稀疏图，反之称为稠密图。如果图中边集为空，则称该图为零图。如果无向图中任何一对顶点之间都有一条边相连，则这个无向图被称为完全图。类似地，如果有向图中任何一对顶点u,u之间都有两条有向边(u, v),(v, u)相连，则称这个有向图为有向完全图。对于一个图，如果以任意一个点为起点，在图上沿着边走都可以到达其他所有点（有向图必须沿有向边的方向），那么这个图就是连通图。显然完全图一定是连通图。

四．图的基本属性和度量（Properties and Measures）
1.节点（Node）
度（Degree）：与节点 Vi 连接的节点数量。
      在无向图中，顶点的度是指某个顶点连出的边数。例如在下图中，顶点 b 的度数为3，顶点 a 的度数为4。

       在有向图中，和度对应的是入度和出度这两个概念。顶点的入度是指以该顶点为终点的有向边数量；顶点的出度是指以顶点为起点的有向边数量。需要注意的是，在有向图里，顶点是没有度的概念的。例如在下图中，顶点 a 的入度为1，出度为3；顶点 c 的入度为2，出度为2。

 

度的性质：
        在无向图或有向图中，顶点的度数总和为边数的两倍，而在有向图中，有一个很明显的性质就是，入度等于出度。

邻居（Neighbors）：与节点 Vi 连接的节点集合。
中心性（Centrality）：度量节点的重要性，有度中心性、特征向量中心性、Katz中心性、中介中心性。
2.节点对（Pairwise Nodes）
行走（Walk）：开始于节点 u，结束于节点 v 的所有可能的序列（Node-Edge-...-Node）。
足迹（Trial）：没有重复边的行走。
路径（Path）：没有重复节点的行走。
测地路径（geodesic path）是指两个节点之间的最短路径。
最短路径（Shortest Path）：两节点间长度最短的路径，可能会超过一条。
3.图（Graph）
n阶邻接矩阵：矩阵 An 的 元素 Ai,j 等于长度为n的 vi - vj 行走的数量。 （下面详细介绍，较为重要）
子图（Subgraph）：由图中部分节点以及这些节点间的边组成的图。
连通分量（Connected Component）：各节点间至少存在一条边可以连通。
连通图（Connected Graph）：只包含一个连通分量，即其自身，那么该图是一个连通图。
直径（Diameter）：各节点之间的最短路径长度中的最大值。
五．图的邻接矩阵（Adjacency Matrix）
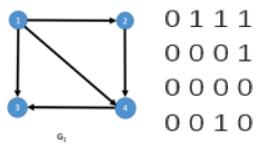
       所谓邻接矩阵存储结构就每个顶点用一个一维数组存储边的信息，这样所有点合起来就是用矩阵表示图中各顶点之间的邻接关系。所谓矩阵其实就是二维数组。对于有n个顶点的图 G=(V,E) 来说，我们可以用一个 n×n 的矩阵 A 来表示 G 中各顶点的相邻关系，如果 vi 和 vj之间存在边（或弧），则 A[i][j]=1 ，否则 A[i][j]=0 。下图为有向图 G1 和无向图 G2 对应的邻接矩阵：

        (需要注意的是，有向图与无向图的矩阵不同，对于无向图，当vi、vj之间由边，则a[i][j]=a[j][i]=1,但是有向图，若i指向j,只有a[i][j]=1,a[j][i]=0)

        一个图的邻接矩阵是唯一的，矩阵的大小只与顶点个数N有关，是一个 N×N 的矩阵。前面我们已经介绍过，在无向图里，如果顶点 vi 和 vj 之间有边，则可认为顶点 vi 到 vj 有边，顶点 vj 到 vi 也有边。对应到邻接矩阵里，则有 A[i][j]=A[j][i]=1　。因此我们可以发现，无向图的邻接矩阵是一个对称矩阵。

       在邻接矩阵上，我们可以直观地看出两个顶点之间是否有边（或弧），并且很容易求出每个顶点的度，入度和出度。

        这里我们以 G1 为例，演示下如何利用邻接矩阵计算顶点的入度和出度。顶点的出度，即为邻接矩阵上点对应行上所有值的总和，比如顶点1出度即为0+1+1+1=3；而每个点的入度即为点对应列上所有值的总和，比如顶点3对应的入度即为1+0+0+1=2。

       接下来我们就先一起学习构造和使用邻接矩阵的方法。邻接矩阵是一个由1和0构成的矩阵。处于第 i 行、第 j 列上的元素1和0分别代表顶点i到j之间存在或不存在一条又向边。

       显然在构造邻接矩阵的时候，我们需要实现一个整型的二维数组。由于当前的图还是空的，因此我们还要把这个二维数组中的每个元素都初始化为0。

        在构造好了一个图的结构后，我们需要把图中各边的情况对应在邻接矩阵上。实际上，这一步的实现非常简单，当从顶点x到y存在边时，我们只要把二维数组对应的位置置为1就好了。

用邻接矩阵来构建图需要如下几步，我们可以用二维数组G来表示一个图
初始化
初始化的过程很简单，只需要把数组初始化为0即可。可以借助memset来快速地将一个数组中的所有元素都初始化为0。（其实定义成全局变量就行了……）

memset(G, 0, sizeof(G));

注意，memset只能用来初始化0和 -1，并且需要加上头文件cstring。

上面的代码等价于：

for (int i = 0; i < N1; i++) { // N1 为数组第一维大小

    for (int j = 0; j < N2; j++) { // N2 为数组第二维大小

        G[i][j] = 0;

    }

}

当然我们平常使用邻接矩阵的时候下标只用 1 到 n 或者 0 到n−1 （这个看题目中点的编号）。

插入边
如果插入一条无向边 (u,v) ，只需要

G[u][v] = 1;

G[v][u] = 1;（由于无向边的特殊性，其必然是对称矩阵）

也可以写成G[u][v] = G[v][u] = 1;。
如果插入一条有向边 (u,v) ，只需要G[u][v] = 1;。

访问边
如果G[u][v] = 1，说明有一条从 u 到 v 的边，否则没有从 u 到 v 的边。

邻接矩阵的使用
#include <iostream>

using namespace std;

const int maxn = 105;

int G[maxn][maxn];

int main() {

    int n, m;

    cin >> n >> m;

    for (int i = 0; i < m; i++) {

        int u, v;

        cin >> u >> v;

G[u][v] = G[v][u] = 1;

    }

    for (int i = 1; i <= n; i++) {

        for (int j = 1; j <= n; j++) {

            cout << G[i][j] << " ";

        }

        cout << endl;

    }

    return 0;

}

当点数较多（多于 5000）时，使用邻接矩阵会超出空间限制，需要使用邻接表。

六．邻接表
邻接表的思想是，对于图中的每一个顶点，用一个数组来记录这个点和哪些点相连。由于相邻的点会动态的添加，所以对于每个点，我们需要用vector来记录。

也就是对于每个点，我们都用一个vector来记录这个点和哪些点相连。比如对于一张有 10 个点的图，vector<int> G[11]就可以用来记录这张图了。对于一条从 a 到 b 的有向边，我们通过G[a].push_back(b)就可以把这条边添加进去；如果是无向边，则需要在G[a].push_back(b)的同时G[b].push_back(a)。（几乎所有地方都要注意有向与无向）

邻接表的优缺点

优点
节省空间：当图的顶点数很多、但是边的数量很少时，如果用邻接矩阵，我们就需要开一个很大的二维数组，最后我们需要存储 n*n 个数。但是用邻接表，最后我们存储的数据量只是边数的两倍。
可以记录重复边：如果两个点之间有多条边，用邻接矩阵只能记录一条，但是用邻接表就能记录多条。虽然重复的边看起来是多余的，但在很多时候对解题来说是必要的。
缺点
当然，有优点就有缺点，用邻接表存图的最大缺点就是随机访问效率低。比如，我们需要询问点 a 是否和点 b 连，我们就要遍历G[a]，检查这个vector里是否有 b 。而在邻接矩阵中，只需要根据G[a][b]就能判断。

因此，我们需要对不同的应用情景选择不同的存图方法。如果是稀疏图（顶点很多、边很少），一般用邻接表；如果是稠密图（顶点很少、边很多），一般用邻接矩阵。

邻接表的实现
#include <iostream>

#include <vector>

using namespace std;

const int maxn = 105;

vector<int> G[maxn];

int main() {

    int n, m;

    cin >> n >> m;

    for (int i = 0; i < m; i++) {

        int u, v;

        cin >> u >> v;

        G[u].push_back(v);

        G[v].push_back(u);

    }

    for (int i = 1; i <= n; i++) {

        cout << i << " : ";

        for (int j = 0; j < G[i].size(); j++) {

            cout << G[i][j] << " ";

        }

        cout << endl;

    }

    return 0;

}

七、图的存储（带权值）
经过上面的介绍，暂且将图的存储分别使用邻接矩阵与邻接表实现。

1.邻接矩阵
在前面，图中的边都只是用来表示两个点之间是否存在关系，而没有体现出两个点之间关系的强弱。比如在社交网络中，不能单纯地用0、1来表示两个人否为朋友。当两个人是朋友时，有可能是很好的朋友，也有可能是一般的朋友，还有可能是不熟悉的朋友。

我们用一个数值来表示两个人之间的朋友关系强弱，两个人的朋友关系越强，对应的值就越大。而这个值就是两个人在图中对应的边的权值，简称边权。对应的图我们称之为带权图。

如下就是一个带权图，我们把每条边对应的边权标记在边上：

        带权图也分成带权有向图和带权无向图。前面学到的关于图的性质在带权图上同样成立。实际上，我们前面学习的图是一种特殊带权图，只不过图中所有边的权值只有1一种；而在带权图中，边的权值可以是任意的。

        用邻接矩阵存储带权图和之前的方法一样，用G[a][b]来表示 a 和 b 之间的边权（我们需要用一个数值来表示边不存在，如0）。同样，对于无向图，这个矩阵依然是对称的。

带权图的邻接矩阵
#include <iostream>

#include <cstring>

using namespace std;

const int maxn = 105;

int G[maxn][maxn];

int sum[maxn];

int main() {

    int n, m;

    cin >> n >> m;

    for (int i = 0; i < m; i++) {

        int u, v, w;

        cin >> u >> v >> w;

G[u][v] = w;

    }

    for (int i = 1; i <= n; i++) {

        for (int j = 1; j <= n; j++) {

            cout << G[i][j] << " ";

        }

        cout << endl;

    }

    for (int i = 1; i <= n; i++) {

        for (int j = 1; j <= n; j++) {

            sum[i] += G[i][j];

        }

    }

    for (int i = 1; i <= n; i++) {

        cout << sum[i] << " ";

    }

    return 0;

}

2.邻接表
用邻接表存储带权图和之前的实现方式略有区别，我们需要用一个结构体来记录一条边连接的点和这条边的边权，然后用一个vector来存储若干个结构体，实际上就是把一个点所连接的点以及这条边的边权"打包"起来放到邻接表中。

结构体的定义举例如下：

struct node {

    int v;  // 用来记录连接的点

    int w;  // 用来记录这条边的边权

};

我们通常把有向图中加入一条边写成一个函数，例如加入一条有向边 (u,v) 、边权为 w ，就可以用如下的函数来实现（我们需要把图定义成全局变量）。

vector<node> G[105];

// 插入有向边

void insert(int u, int v, int w) {

    node temp;

    temp.v = v;

    temp.w = w;

    G[u].push_back(temp);

}

而插入一条无向边，实际上相当于插入两条方向相反的有向边：

// 插入无向边

void insert2(int u, int v, int w) {

    insert(u, v, w);

    insert(v, u, w);

}

带权图邻接表的实现

#include <iostream>

#include <vector>

using namespace std;

const int maxn = 105;

struct node {

    int v;

    int w;

};

vector<node> G[maxn];

void insert(int u, int v, int w) {

    node temp;

    temp.v = v;

    temp.w = w;

    G[u].push_back(temp);

}

int main() {

    int n, m;

    cin >> n >> m;

    for (int i = 0; i < m; i++) {

        int u, v, w;

        cin >> u >> v >> w;

        insert(u, v, w);

    }

    for (int i = 1; i <= n; i++) {

        for (int j = 0; j < G[i].size(); j++) {

cout << i << " " << G[i][j].v << " " << G[i][j].w << endl;

        }

    }

    return 0;

}

一般还有第三种存储方式：

存储为边列表：

1   2

1   3

1   4

2   3

3   4

...

我们存储有边连接的每一对节点的 ID。

图可能包含一些扩展：包括节点/边上加标签、加上与节点/边相关的特征向量

八．高级的图结构
以上介绍的是简单图结构及其属性，但是真实世界中的图要更加复杂。

异质图（Heterogeneous Graphs）
图中的每个节点和边都有多种类型，如下图所示：

二部图（Bipartite Graphs）
节点分为两类，只有不同类的节点之间存在边。比如，消费者和商品的购买关系。

多维图（Multi-dimensional graph）
节点之间可以同时存在多种类型的关系，需要使用多个邻接矩阵表示。比如消费者和商品之间的点击、购买和评论等关系。

符号图（signed Graphs）
节点之间同时存在正向和负向的边。比如社交网络中，关注某个人和屏蔽某个人是相对的（+1，-1），暂时未有过交互的为0。

超图（Hypergraphs）
每一条边可以包含两个以上的节点所构成的图。比如一篇论文可能有两个以上的作者产生关系。

动态图（Dynamic Graphs）
考虑节点和边随时间的变化的图。

 
————————————————
版权声明：本文为CSDN博主「೭౨」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/Mitsui14wung/article/details/118618959